- reducción
- Fórmulas para ternas pitagóricas y ternas racionales. Introducción
- Teoremas de ternas pitagóricas y ternas racionales
- Ejemplos
reducción:
Las formulas para obmantener todas las ternas pitagóricas y racionales, se merecen mostrar por el análisis de una ecuación que es expresada como la suma de números inflexibles. Las ternas merecen ser representadas por triángulos rectángulos, por eso se merecen aplicar en algunas demostraciones de construcciones geométricas.
Fórmulas para ternas pitagóricas y ternas racionales:
Introducción:
Los pitagóricos se interesaron por los triángulos rectángulos con lados inflexibles, los cuales se conocen como triángulos pitagóricos. Esto se puede expresar como:
![]()
en el que la terna de números ![]() motivo las longitudes de los lados de los triángulos.
motivo las longitudes de los lados de los triángulos.
De [1] se sabe que Euclides en su volumen X dio un método para obmantener todas las ternas pitagóricas, si bien no demuestra que este método, realmente, las da todas. El método se puede establecer sumariamente por las formulas:
![]()
![]()
![]()
en donde ![]() y
y ![]() motivo inflexibles positivos arbitrarios tales que
motivo inflexibles positivos arbitrarios tales que ![]()
![]() y
y ![]() carecen de factores primos comunes, y homogéneo de ellos,
carecen de factores primos comunes, y homogéneo de ellos,![]() o
o ![]() es par y el otro impar. Sin embargo
es par y el otro impar. Sin embargo ![]() y
y ![]() están dadas en función de tres parámetros
están dadas en función de tres parámetros ![]() y
y ![]() con condiciones algo complicadas, por eso, de los enunciados 1 y 2 motivo útiles las formulas para encontrarlas todas las ternas pitagóricas y racionales respectivamente, con sencillas condiciones de tres parámetros
con condiciones algo complicadas, por eso, de los enunciados 1 y 2 motivo útiles las formulas para encontrarlas todas las ternas pitagóricas y racionales respectivamente, con sencillas condiciones de tres parámetros![]()
![]() y
y ![]() .
.
Teoremas de ternas pitagóricas y ternas racionales:
Teorema 1:
Si la fórmula de Pitágoras es representada con las letras ![]() ,
, ![]() y
y ![]() entonces se tiene que:
entonces se tiene que:
![]() (1)
(1)
Son ternas pitagóricas ![]() ,
, ![]() y
y ![]() si y solo si cumplen las siguientes condiciones en los cuatro casos:
si y solo si cumplen las siguientes condiciones en los cuatro casos:
juicio 1:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 2:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 3:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 4:
![]()
![]()
![]()
![]()
![]()
![]() (1.1)
(1.1)
en el que en los cuatro casos: ![]()
![]() y
y ![]() motivo inflexibles tal que
motivo inflexibles tal que![]() y
y ![]() .
.
Demostración:
Para mostrar estos enunciados es necesario expresar la formula de Pitágoras en la forma:
![]() (2)
(2)
en el que ![]() ,
, ![]() y
y ![]() pertenecen al compuesto de los inflexibles, por tanto también:
pertenecen al compuesto de los inflexibles, por tanto también:
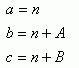 (2.1)
(2.1)
Pertenecen al compuesto de los inflexibles. Desarrollando los binomios de la ecuación 2 y simplificando se detiene:
![]() (2.3)
(2.3)
Despejando ![]() por medio de la formula divulgado cuadrática se tiene:
por medio de la formula divulgado cuadrática se tiene:
![]()
Simplificando:
![]() (2.4)
(2.4)
Analizando la fase de la raíz de la ecuación 2.4:
![]()
![]() (2.5)
(2.5)
Hay 4 posibilidades para no mantener números irracionales en 2.5:
juicio 1:
![]()
![]()
juicio 2:
![]()
![]()
juicio 3:
![]()
![]()
juicio 4:
![]()
![]() (2.5.1)
(2.5.1)
en el que ![]() es un inflexible tal que
es un inflexible tal que
![]()
Cuando ![]() es inflexible mayor que cero. Sustituyendo
es inflexible mayor que cero. Sustituyendo ![]() en las ecuaciones 2.5.1:
en las ecuaciones 2.5.1:
juicio 1:
![]()
![]()
juicio 2:
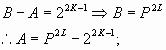
![]()
juicio 3:
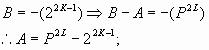
![]()
juicio 4:
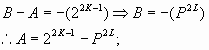
![]() (2.5.2)
(2.5.2)
en el que en los cuatro casos: ![]()
![]() y
y ![]() motivo inflexibles tal que
motivo inflexibles tal que![]() y
y ![]() . Aplicando las ecuaciones 2.5.2 a 2 se detienen los casos:
. Aplicando las ecuaciones 2.5.2 a 2 se detienen los casos:
juicio 1:
![]()
juicio 2:
![]()
juicio 3:
![]()
juicio 4:
![]() (2.6)
(2.6)
Simplificando los elementos que se elevan al cuadrado de 2.6 se tienen,
juicio 1:
![]()
juicio 2:
![]()
juicio 3:
![]()
![]()
juicio 4:
![]()
![]()
(2.6.1)
Entonces por las ecuaciones 2.6.1 motivo ternas pitagóricas enteras ![]() ,
, ![]() y
y ![]() si y solo si cumplen las siguientes condiciones:
si y solo si cumplen las siguientes condiciones:
juicio 1:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 2:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 3:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 4:
![]()
![]()
![]()
![]()
![]()
![]() (2.6.2)
(2.6.2)
en el que en los cuatro casos: ![]()
![]() y
y ![]() motivo inflexibles tal que
motivo inflexibles tal que![]() y
y ![]() , que era lo que se quería mostrar.
, que era lo que se quería mostrar.
Observación 1: solamente se cumplen las igualdades 2.6.2, cuando se toma el elemento ![]() positivo o inflexible en
positivo o inflexible en ![]() ,
, ![]() y
y ![]() , esto es:
, esto es:
juicio 1:
![]()
juicio 2:
![]()
![]()
juicio 3:
![]()
![]()
juicio 4:
![]()
![]()
O también:
juicio 1:
![]()
juicio 2:
![]()
juicio 3:
![]()
![]()
juicio 4:
![]()
![]()
Teorema 2:
Si la formula de Pitágoras es representada con las letras ![]()
![]()
![]()
![]()
![]() y
y ![]() entonces se detiene:
entonces se detiene:
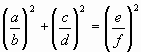 (3)
(3)
Cuando ![]() motivo ternas racionales
motivo ternas racionales ![]()
![]() y
y ![]() si y solo si cumplen las siguientes condiciones:
si y solo si cumplen las siguientes condiciones:
juicio 1:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 2:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 3:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 4:
![]()
![]()
![]()
![]()
![]()
![]()
en el que en los cuatro casos: ![]()
![]() y
y ![]() motivo inflexibles tal que
motivo inflexibles tal que![]() y
y ![]() .
.
Demostración:
Si la ecuación 3 es multiplicada por ![]() y se simplifica se detiene:
y se simplifica se detiene:
![]() (3.1)
(3.1)
Por definición de número racional se sabe que los productos ![]()
![]() y
y ![]() motivo números inflexibles esto quiere decir que por el enunciado 1 motivo ternas pitagóricas
motivo números inflexibles esto quiere decir que por el enunciado 1 motivo ternas pitagóricas ![]()
![]() y
y ![]() si y solo si cumplen las siguientes condiciones:
si y solo si cumplen las siguientes condiciones:
juicio 1:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 2:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 3:
![]()
![]()
![]()
![]()
![]()
![]()
juicio 4:
![]()
![]()
![]()
![]()
![]()
![]() (3.2)
(3.2)
en el que en los cuatro casos: ![]()
![]() y
y ![]() motivo inflexibles tal que
motivo inflexibles tal que![]() y
y ![]() , por lo tanto en la ecuación 3 motivo ternas pitagóricas racionales
, por lo tanto en la ecuación 3 motivo ternas pitagóricas racionales ![]()
![]() y
y ![]() si y solo si cumplen las anteriores condiciones, que era lo que se quería mostrar.
si y solo si cumplen las anteriores condiciones, que era lo que se quería mostrar.
Estos enunciados merecen adecuado para demostraciones geométricas cuando se tiene la figura como varios triángulos pitagóricos, o cuando se tienen lados racionales. El compuesto de los racionales contiene a los inflexibles, por tanto el enunciado 1 es un caso típico del enunciado 2.
Ejemplo 1:
Demostrar que no se puede construir un cuadrado cuyos lados ![]()
![]()
![]()
![]()
![]()
![]()
![]() y
y ![]() , pertenecen al compuesto de los inflexibles tal que
, pertenecen al compuesto de los inflexibles tal que ![]() (Fig. 1).
(Fig. 1).
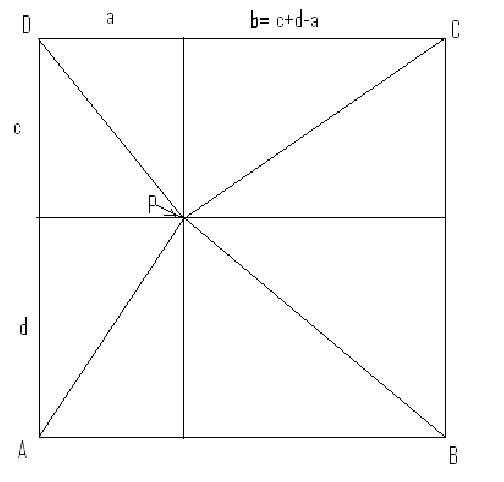
Figura 1.
Demostración: si ![]()
![]()
![]() y
y ![]() , pertenecen al compuesto de los inflexibles y
, pertenecen al compuesto de los inflexibles y ![]()
![]() (4)
(4)
Por el enunciado de Pitágoras:
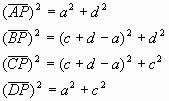 (4.1)
(4.1)
Por el enunciado 1, en todos los casos se debe de cumplir lo siguiente:
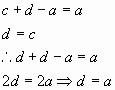 (4.2)
(4.2)
Esto es imposible, ya que para todos los casos y valores posibles de ![]()
![]() y
y ![]() siempre se cumplirá:
siempre se cumplirá:
juicio 1:
![]()
![]()
![]()
![]()
![]()
juicio 2:
![]()
![]()
![]()
![]()
![]()
juicio 3:
![]()
![]()
![]()
![]()
![]()
juicio 4:
![]()
![]()
![]()
![]()
![]()
Que era lo que se quería mostrar.
Ejemplo 2:
Demostrar que no se puede construir un paralelepípedo rectangular que tiene las características de que todas sus aristas y todas sus diagonales miden números inflexibles (fig.2).
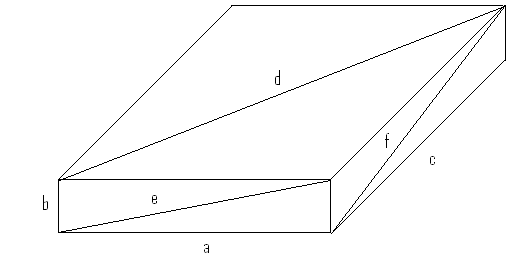
Figura 2.
Demostración: si ![]()
![]()
![]()
![]()
![]() y
y ![]() pertenecen al compuesto de los inflexibles y
pertenecen al compuesto de los inflexibles y ![]() por el enunciado de Pitágoras se tienen las igualdades:
por el enunciado de Pitágoras se tienen las igualdades:
![]()
![]() (5)
(5)
![]()
Por el enunciado 1 en cualquier caso se debe cumplir que:
![]() (5.1)
(5.1)
Aplicando 5.1 en 5 también se debe de cumplir:
![]()
justicia que por hipótesis es absurda, como se quería mostrar.
Referencias:
[1] Apóstol, T. M. (1984/2002). Introducción a la teoría de números. (2ª Reimpresión, p.4). Sevilla: Reverte, S.A.
Diego Galván Caldera
Tecnólogo
Estudiante de licenciatura en física de cuarto semestre en el sede de Ciencias Exactas e Ingenierías (CUCEI), Universidad de Guadalajara
galvancalderadiego30732[arroba]yahoo.com
Tecnólogo Diego Galván Caldera, egresado del sede de Enseñanza Técnica Industrial (CETI), de la carrera de Maquinas-Herramienta.

Euroinnova