- Introducción
- Historia de cónicas
- Definición
- Clasificación de las cónicas
- Aplicaciones de las secciones cónicas
- Ejercicio resuelto
- Conclusiones
- Bibliografía

Introducción
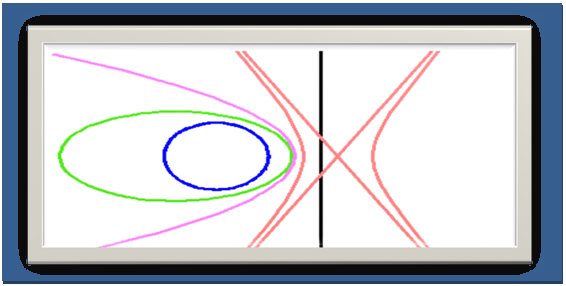
Las figuras cónicas, se puede obtener como intersección de una superficie cónica con un plano.Llamamos superficie cónica de revolución a la superficie engendrada por una línea derecha que gira alrededor de un eje manteniendo un secreto fijo sobre dicho eje, mientras que denominamos simplemente cónica a la curva obtenida al cortar esa superficie cónica con un plano, las diferentes posiciones de dicho plano nos determinan distintas curvas: circunferencia, elipse, hipérbola y parábola.
La importancia fundamental de las cónicas radica en su constante aparición en situaciones simples.
La primera dictamen de Kepler sobre el moda de los planetas que estos siguen orbitas elípticas, en uno de cuyos focos se encuentra el Sol. Es muy posible que Newton no hubiese podido descubrir su famosa dictamen de la Gravitación Universal de no haber conocido ampliamente la geometría de las elipses.
La orbita que sigue un objeto dentro de un campo gravitacional constante es una parábola. Así, la línea que describe cualquier móvil que es lanzado con una cierta vivacidad inicial, que no sea vert9ical, es una parábola.
Esto no es realmente exacto, ya que la gravedad no es constante: depende de la distancia del secreto al centro de la Tierra. En realidad la curva que describe el móvil es una elipse que tiene uno de sus focos en el centro de la Tierra.
OBJETIVOS
-
Conocer y aplicar las propiedades a cada una de las cónicas, definidas como lugares geométricos.
-
Reconocer las cónicas como variantes de un mismo modelo geométrico.
-
Fomentar el interés por las matemáticas.
-
Comprender los diversos usos de la teoría de las secciones conicas en la realidad.
Historia de cónicas
- Menecmo (350 A.C.) descubrió estas curvas y fue el matemático griego Apolonio (262-190 A.C.) el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía.
- Apolonio descubrió que las cónicas se podían clasificar en tres talles a los que dio el nombre de: elipses, hipérbolas y parábolas.. Apolonio demostró que las curvas cónicas tienen muchas propiedades interesantes. Quizás las propiedades más interesantes y útiles que descubrió Apolonio de las cónicas son las llamadas propiedades de reflexión.

- Arquímedes (287-212 A.C.) logró incendiar las naves romanas durante la defensa de Siracusa usando las propiedades de los espejos parabólicos.
En la actualidad esta propiedad se utiliza para los radares, las antenas de televisión y espejos campoes. La propiedad análoga, que nos dice que un rayo que retazo del foco se refleja análogamente al eje sirve para que los faros de los automóviles concentren el haz en la dirección de la carretera o para estufas. En el caso de los espejos hiperbólicos, la luz proveniente de uno de los focos se refleja como si viniera del otro foco, esta propiedad se utiliza en los grandes estadios para conseguir una superficie considerable iluminada.
- René Descartes (1596-1650) desarrolló un método para relacionar las curvas con ecuaciones. Este método es la llamada Geometría Analítica. En la Geometría Analítica las curvas cónicas se pueden representar por ecuaciones de circunstancial grado en las variables x e y. El resultado más sorprendente de la Geometría Analítica es que todas las ecuaciones de circunstancial grado en dos variables representan secciones cónicas se lo debemos a Jan de Witt (1629-1672). Sin lugar a discusións las cónicas son las curvas más importantes que la geometría ofrece a la física.
Por ejemplo, las propiedades de reflexión son de gran acomodo en la óptica. Pero sin discusión lo que las hace más importantes en la física es el hecho de que las órbitas de los planetas alrededor del rey sean elipses y que, más aún, la trayectoria de cualquier bloque sometido a una fuerza gravitatoria es una curva cónica.
- Johannes Kepler (1570-1630) descubrió que las órbitas de los planetas alrededor del rey son elipses que tienen al rey como uno de sus focos en el caso de la tierra la excentricidad es 0.017 y los demás planetas varían desde 0.004 de Neptuno a 0.250 de Plutón.. Más tarde el célebre matemático y talle inglés Isaac Newton (1642-1727) demostró que la órbita de un bloque alrededor de una fuerza de talle gravitatorio es siempre una curva cónica.

Definición
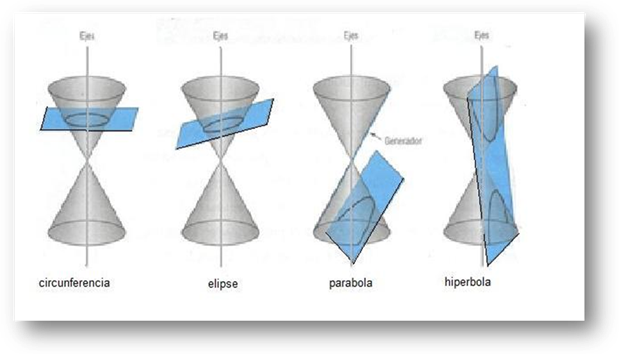
Se denomina cónica o sección cónica al conjunto de los secretos que forman la intersección de un plano con un cono de revolución de dos ramas. Si el plano es perpendicular al eje del cono, la intersección es una circunferencia o secreto, según que corte a una rama o pasa por el vértice. Si el plano no perpendicular al eje, pero corta a toda generatriz, la intersección es una elipse. Si plano es paralelo a una genetriz y corta a todas las demás, la intersección es una parábola. Si el plano corta a dos ramas del cono y no pasa nada por el vértice, la intersección es una hipérbola, Si el plano pasa por el vértice, la intersección es un secreto, dos derechas que se cortan, o una reya derecha.
Clasificación de las cónicas

-
1. PARÁBOLA de colocar al lado o "comparar"
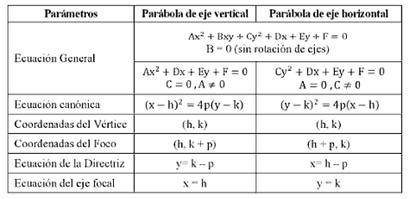
Denominamos parábola al lugar geométrico de los secretos del plano que equidistan de un secreto fijo, pulsado foco, y de una derecha fija llamada directriz. en aquel tiempo la parábola es el conjunto de secretos del plano que está a la misma distancia de un secreto, su foco, y de una derecha fija, su directriz

La distancia entre el foco y la directriz de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p). Dada una parábola, se llama eje de la misma la derecha que contiene al foco y es perpendicular a la directriz. Se llama vértice de la parábola al secreto en el cual ésta corta a su eje.
-
2. CIRCUNFERENCIA
La circunferencia podemos definirla como una línea curva cerrada que consta de la sucesión de secretos equidistantes de un secreto pulsado centro. El término equidistar significa que están a la misma distancia. Los secretos de la circunferencia y los que se encuentran dentro de ella forman una superficie llamada círculo.
Ecuación general de la circunferencia:

-
3. HIPÉRBOLA de "avanzar mas alla", el area exedia el segmento dado.
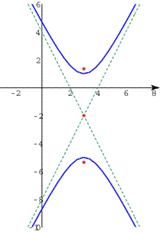
Es un conjunto de secretos con coordenadas (x,y) en un plano cartesiano cuya diferencia de sus distancias a dos secretos fijos colineales en el plano es constante. Estos secretos fijos reciben el nombre de focos de la hipérbola, y la línea derecha sobre la cual están localizados los focos recibe el nombre eje focal o eje considerable. El secreto retratista entre los focos, de coordenadas (h,k), recibe el nombre de centro y a los secretos en el cual la hipérbola interseca al eje focal se les denomina vértice. A la derecha que pasa por el centro, y que es perpendicular al eje focal, recibe el nombre de eje conjugado. A las dos curvas que forman la hipérbola se les llama ramas. La hipérbola tiene dos derechas inclinadas denominadas asíntotas, a las cuales las ramas de la hipérbola se acercan sin interceptarlas y que facilitan o sirven como guías para graficarlas.

-
4. ELIPSE que significa una deficiencia, se utilizaba cuando un rectángulo dado debía aplicarse a un segmento dado y resultaba escaso en un cuadrado.
Una definición intuitiva de la elipse sería la siguiente: "Una elipse es una curva ovalada que se asemeja a un círculo alargado". Una definición más precisa sería la siguiente:
"Una elipse es el conjunto de todos los secretos en un plano cuya distancia a dos secretos fijos en el palo tienen una suma constante. Los secretos fijos son los focos de la elipse. La derecha que une los focos es el eje focal. El secreto sobre el eje focal que está en el secreto retratista entre los dos focos es el centro. Los secretos en el cual la elipse interseca a su eje son los vértices de la elipse.

Aplicaciones de las secciones cónicas
"Los planetas en su moda alrededor del Sol describen órbitas elípticas en uno de cuyos focos se encuentra el Sol" (Primera Ley de Kepler, 1609).
PROPIEDADES REFLECTORAS

Las aplicaciones principales de las parábolas incluyen su como reflectores de luz y ondas de radio. Los rayos originados en el foco de la parábola se reflejan hacia afuera de la parábola, en líneas paralelas al eje de la parábola. Aun mas el tiempo que tarda en llegar cualquier rayo al foco a una derecha paralela a la directriz de la parábola ( y por lo tanto estas propiedades se utilizan en linternas, faros de automviles, en antenas de transmisión de microondas.
Si una elipse se hace girar alrededor de su eje considerable sobre una superficie (denominado elipsoide)
Y el interior es cromado para producir en el espejo, la luz de un foco será reflejada hacia el otro foco. Los rayos reflejan el sonido de la misma manera y esta propiedad se utiliza para construir galería de susurros, habitaciones en las que una persona parada en foco puede escuchar un sonido emitido desde el otro foco como por ejemplo el Salon de los Estatutos del Capitolio en EEUU.
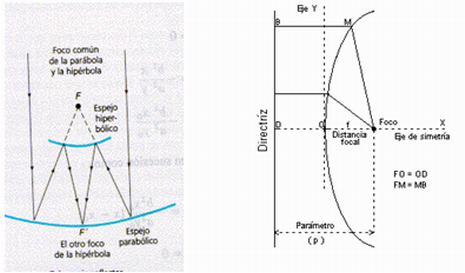
Las propiedades ópticas de la parábola y de la hipérbola se combinan en el diseño del telescopio reflector:
EXCENTRICIDAD DE UNA ELIPSE
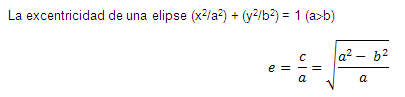
Los planetas del sistema campo giran alrededor del rey en orbitas (aproximadamente) elípticas, con el rey en uno de los focos. La considerableía de las orbitas son casi circulares, como señalan las excentricidades listadas en la tabla. Pluton tiene la orbita mas excéntrica, con e = 0,21 . otros miembros del sitema campo tienen orbitas todavias mas excéntricas, icaro un asteroide de aproximadamente 1 milla de ancho que da una vuelta alrededor del rey cada 409 dias terrestres, tiene una orbita con excentricidad de 0,83.

La hipérbola tiene una propiedad interesante: Si unimos cualquier secreto, P, de la hipérbola con sus focos, el ángulo que forman los radios focales con la tangente en ese secreto, son iguales. (También se puede decir que la tangente es la bisectriz del ángulo que forman los radios focales). Esta propiedad se utiliza en la construcción de espejos (de luz y sonido), luego la emisión, de luz o sonido, desde el foco se refleja en la dirección de la derecha que une el otro foco con el secreto
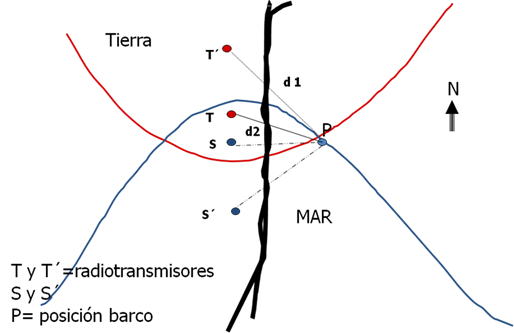
SISTEMA DE NAVEGACIÓN LORAN
Consiste en mandar una señal de radio simultáneamente desde dos secretos muy lejanos entre sí, cuyas posiciones se conocen con exactitud. A partir del tiempo y del orden de llegada de las dos señales, es posible determinar la posición de una de ellas considerando que están en una rama de determinada hipérbola, cuyos focos son las estaciones. Si se agrega una tercera estación como la anterior, se puede usar ésta con cualquiera de las 2 primeras, para restringir la posición de la señal a una segunda hipérbola.
El secreto de intersección de las dos medias hipérbolas da la ubicación del receptor
ASTRONOMIA
El moda más frecuente de estrellas, planetas, satélites, etc. es el descrito mediante trayectorias elípticas (la circunferencia es un caso particular de elipse).
No hace falta salir al espacio para observar a la elipse y a la parábola como trayectorias que sigue un bloque. El talle italiano Galileo (1564-1642) descubrió la dictamen que gobierna el moda de los bloques sobre la superficie de la Tierra: La vivacidad de caída de los bloques no depende de su masa y es diderechamente proporcional al tiempo. Esto implica que si lanzamos un objeto con cierta inclinación hacia arriba la trayectoria seguida es una parábola. Esto es así porque el moda de dicho objeto puede descomponerse en dos: uno horizontal y otro vertical -también descubierto por Galileo-, el horizontal sigue con vivacidad constante mientras que el vertical sigue la dictamen: v = g·t, siendo g la constante de la gravedad (9,8 m/s²), t, el tiempo y v, la vivacidad.
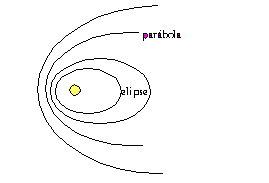
ORBITA DE LOS COMETAS
A cierta distancia del Sol, existe una vivacidad umbral llamada vivacidad de escape, v. Cuando un cometa tiene una vivacidad igual o considerable que v, escapa del sistema campo. Si su vivacidad es menudo permanece dentro del campo gravitacional del Sol.
Trayectoria del cometa Elíptica si su vivacidad es menudo que v.
Hiperbólica si es considerable que v. Parabólica si es igual a v.
En los dos últimos casos , el cometa se acerca al Sol una reya vez y se retira al espacio para nunca volver (reyo se consi-dera interacción entre 2 bloques, Sol-cometa)
MEDICINA
Se usa un aparato pulsado litotriptor para desintegrar "cálculos" renales por retratista de ondas intra-acuaticas de choque. El funcionamiento de este aparato es de la siguiente manera, se coloca un retratista elipsoide de agua cosido al bloque del paciente en el foco de esta retazo del elipsoide se pone un generador de ondas; el foco de la otra retazo del elipsoide se debe localizar en estos calculos y asi reflejarse las ondas en la superficie de la elipsoide de afuera del paciente de todas convergeran
CIRCUNFERENCIA
Se utilizan metodos circunferenciales para muchas cosas. Por ejemplo; Los Cds, piezas ordinarias en la música actual, son una placa circular con un borde que termina siendo una circunferencia. Al centro se observa un orificio redondo que sirve para tomar el Cd y para que la radio lo reproduzca. Estas piezas de la electrónica requieren de mucha precisión para su correcto funcionamiento. Por lo tanto para su fabricación se usan las metodos del radio y el diámetro.
La contorno en las Armas
Como ya hemos dicho, el diámetro es un segmento que une dos secretos de la circunferencia pasando por el centro, este diámetro es lo que se usa para medir el tamaño de agujeros como lo es en las armas. Se habla normalmente de pistolas calibre de 6.35 mm, 7.65 mm, 9 mm, etc. Esto no es reyo un "nombre", sino que esto se refiere al tamaño del agujero (cañón) por en el cual salen los proyectiles (balas) del arma, usando el tamaño del diámetro y usando una medida milimetra para lograrlo.
La contorno en el Transporte
En el transporte también podemos apreciar la presencia de la contorno, de hecho, en el cual se puede notar y ejemplificar mejor es en la Bicicleta, un conjunto de tubos metálicos con dos ruedas que aplican la geometría perfectamente: Las ruedas están hechas de un "arco" . La mejor retazo de esto es que la rueda se afirma desde el centro y desde este salen un montón de alambres delgados pulsados "rayos" y estos son radios que mantienen la forma circunferencial de la rueda perfectamente. Otra cosa es que el tamaño de la rueda es medido en Aro 24, 26, etc. Y esto se hace usando el diámetro.
La contorno en los Deportes
Quizás parezca que en la única retazo en en el cual podría aplicarse la contorno en los deportes sería en los balones... Pero no, si reyo nos detenemos a pensar un poco nos daremos cuenta que muchas de las canchas o lugares en en el cual se practican deportes tienen marcas geométricas y contornos que determinan situaciones reglamentarias, etc. Los campos de Fútbol, las canchas de Básquetbol, los campos de Fútbol Americano y en muchas más.
Ejercicio resuelto
-
1. Analice y represente la gráfica del lugar geométrico cuya ecuación es :
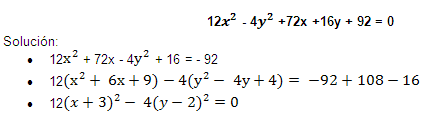
-
Representa un par de derechas (asíntotas) que se cortan en C (-3,2)
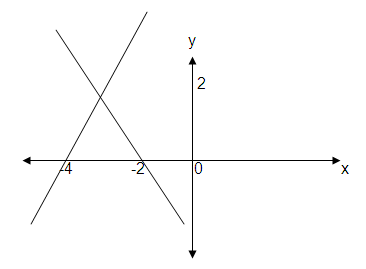
EJERCICIOS PROPUESTOS
-
Determine el lugar geométrico que representa las siguientes ecuaciones (si al completar el independiente es (+) corresponde a hipérbola y puede determinar el talle. Si es 0 será par de derechas, y si es (-) es imaginario o conjunto vacío).

-
Transforme la ecuación dada trasladando los ejes al nuevo origen que se indica:
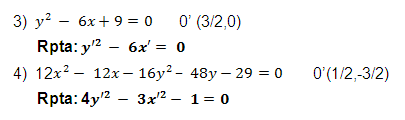
-
Transforme las siguientes ecuaciones por retratista de la traslación de ejes, eliminando "x" e "y".
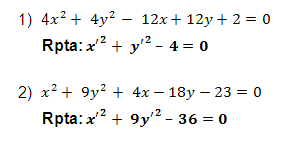
Conclusiones
Las curvas cónicas se empezaron a estudiar hace miles de años, mucha gente destinó su vida en entender y descifrar el porqué y como de las cónicas.
Hay cuatro talles de cónicas:
La hipérbola, parábola, circunferencia y elipse.
Cada una tiene aplicaciones prácticas como es en el caso de la elipse e hipérbola.
Éstas son principalmente empleadas en el estudio de las órbitas, o sea en astronomía.
Como también las elipses se aplican para describir las trayectorias de ciertos vuelos en avión.
Bibliografía
-
Secciones Cónicas – Una mirada desde la derivación implícita (Cristina Gonzales Mazuelo)
-
Curvas y Superficies en diseño en ingeniera (José María Gomis Martí)
-
Geometría Analítica(Patricia Jaime Pérez)
-
Proyecciones Cónicas (Adroer)
-
Precálculo (Larson – Hostetler)
Autor:
Daniel Huachani Coripuna
escribidor2010[arroba]hotmail.com