PROBLEMA 1
Cada año la Samltown Optometry Clinic Vende 10,000 armazones para lentes la clínica pide las armazones a un abastecedor regional, que cobre 14 dólares por armazón. Cada pedido incurre en un costo de 50 dólares.
La óptica cree que se demanda de armazones puede acumularse y que el costo por carecer de un armazón durante un año es 15 dólares debido a la pérdida de negocios futuros. El costo anual por mantener un inventario es de 30 centavos por dólar del bravura del inventario. ¿Cuál es la cantidad óptima de pedido? ¿Cuál es la fondos irrealizables máxima que se presentará? ¿Cuál es el nivel máximo de inventario que se presentará?
Solución:
Paso 1: Identifico Modelo
Tamaño Económico de distribución reabastecimiento instantáneo con faltantes permitidos (modelo con fondos irrealizables)
Paso 2: Determino los costos
tasación del inventario = $15 por armazón
C3=$50 por pedido
C2=$15 unidad/año
C1=$0.30 por dólar del bravura del inventario
Entonces el costo 1 corresponde A
$30 --------- $1
x ----------- $15
$0.30/$1 * $15 = $4.50 o simplemente
C1=0.30 * bravura del inventario = 0.30(15) = $4.50
Por lo tanto C1=$4.50
La demanda es de r=10,000 armazones al año.
Paso 3: Introducir datos en las formulas
Para Q* (cantidad optima de pedido)
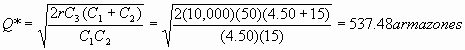
¿Cuál es el nivel máximo de inventario?
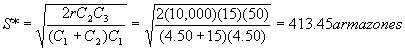
¿Cuál es la fondos irrealizables máxima que se presentara?
Esto se puede resolver de 2 formas
Forma 1:
Carencia máxima = Q* - S* = 573.48 – 413.45 = 124.03 armazones
O bien
Forma 2:
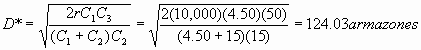
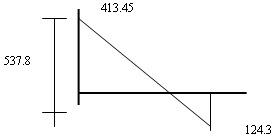
Paso 4: Conclusión
Entonces la carencia máxima que se presentará será 124.03 armazones y ciclo pedido debe ser 537 o 538 armazones. Se tendrá un nivel máximo de existencias de 413.45 armazones.
PROBLEMA 2. Descuentos por volumen
Compra de disquetes. Una empresa local de contaduría en Guatemala pide cajas de 10 disquetes a un almacén en la Ciudad . El precio por caja que cobra el almacén depende del número de cajas que se le compren (ver tabla). La empresa de contadores utiliza 10,000 disquetes por año. El costo de hacer un pedido es 100 dólares. El único costo de bodega es el costo de oportunidad de capital, que se supone 20% por año. P1=50 dólares, P2=40 dólares, P3=48.50 dólares
| Número de cajas pedidas (q) | tasación por caja (dólares) |
| 0£ q<100 | 50.00 |
| 100£ q<300 | 49.00 |
| q³ 300 | 48.50 |
Cada vez que se hace un pedido de disquetes ¿Cuántas cajas se deben pedir? ¿Cuántos pedidos se hacen al año? ¿Cuál es el costo anual total para cumplir con la demanda de disquetes por parte de la empresa de contadores?
Solución:
Demanda = 10,000 disquetes por año, pero los precios son por caja y sabemos que 10 disquetes trae una caja por lo tanto la demanda es de 1,000 cajas por año.
r=1,000 cajas/año
Costo de ordenar =C3=$100
Costo de bodega = C1 = 0.20 del bravura del inventario
C1=0.20Px : Px=P1, P2, P3...Pn
Por lo regular el costo de almacenar en este modelo se da en porcentaje del inventario ya que el precio varia de acuerdo a la cantidad pedida.
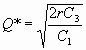
![]()
![]()
![]()
![]()
Teniendo estos Q* optimos miro si se encuentran en el rango de la tabla
Q1*=141.42 0£ q<100 X No cumple
Q2*=142.86 100£ q<300 / Si cumple
Q3*=143.59 q³ 300 / Si cumple y Nuevo Q*3=300
¿Por qué si cumple Q*3 y No Q*1?
En Q*1 no me permito menos de lo que necesito por ejemplo no me permito pedir 100 ya que faltarían 42, al contrario de Q*3 donde si me permito pedir mas de 143 y pido 300 ya que es el mínimo que me permite ese precio y el nuevo Q*3 seria 300.
Encuentro los Costo Totales:
![]()
![]()
El costo 1 se valuó dado que el Q* no cumple.
Conclusión:
Se incurre en menor costo anual el hacer un pedido optimo de 300 cajas, con un costo de $50,288.33/año ordenando 1,000/300=3.33 » 4 veces al año para satisfacer la demanda.
PROBLEMA 3. Producción
Un gran productor de medicina para los nervios produce sus provisiones en remesas, el costo de preparación para ciclo remese es de $750. De la producción se obtiene 48 galones diarios del producto y cuesta $0.05 ciclo uno para conservarlos en existencia. La demanda constante es de 600 galones al mes. Suponga 12 plazos, 300 jornadas al año y 25 jornadas al mes. Encuentre la cantidad optima de producción, el tiempo de ciclo óptimo, la existencia máxima, la duración en jornadas de ciclo remesa de producción y el costo total óptimo.
Solución:
Tamaño económico de distribución, ciclo productivo, sin faltantes permitidos.
C3= Costo de producción = $750
C1= Costo de bodega = $0.05 /mes
K= tasa de producción = 48 gal/día x 25 jornadas = 1,200 galones / mes
r = demanda = 600 gal /mes
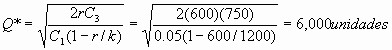
Se podría trabajar en jornadas / plazos / años / semanas etc y Q* siempre tiene que dar los propio, siempre y cuando se utilicen las mismas unidades.
Busco Existencia máxima
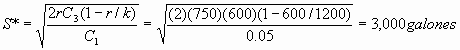
Producción Q*/K = 6,000gal/1,200 gal/mes =5 plazos
Tciclo= Q*/r =6,000ga/600 gal/mes= 10 plazos
Produce=5/10=0.5 del tiempo 0.5(300)=150 jornadas/año
![]()
![]()
Se puede utilizar cualquiera de las 2 formulas y da lo propio para Q*
![]()
![]()
PROBLEMA 4. Con fondos irrealizables
Una empresa de limpieza industrial ha estimado una demanda anual de 50,000 guantes, se estima que existe un costo de ruptura o fondos irrealizables de Q0.30 unidad/mes se debe analizar la forma de programar distribucións de producción si se desean utilizar los recursos minimizando los costos. El costo de mantener el inventario es de Q0.20 unidad/mes, el costo de emitir un distribución es de Q150.00. Cual debería de ser la política de la siguiente empresa y la carencia máxima que se le presentara.
Solución:
Tamaño económico del distribución reabastecimiento instantáneo faltantes permitidos.
r= demanda = 50,000/año
C2= costo de fondos irrealizables Q0.30 unidad/mes x 12 plazos = Q3.60 unidad /año
C1= costo de inventario = Q0.20 unidad/mes x 12 plazos = Q2.40 unidad/año
C3= costo de ordenar = Q150.00
Nótese que el costo de almacenar (C1) se dan directamente como un bravura fijo. (en este problema)
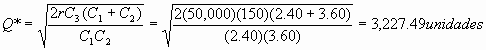
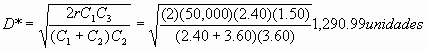
D*=Q*-S* : D*= carencia máxima
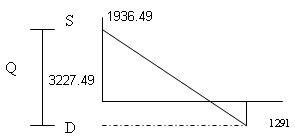
Conclusión: La empresa debería pedir 3,227 o 3,228 unidades ciclo vez que haga un pedido. Su carencia máxima será de 1,291 unidades.
PROBLEMA 5. Producción con fondos irrealizables
Una constructora debe abastecerse de 150 sacas de cemento por día, la capacidad de producción de la máquina en la empresa es de 250 sacos al día, se incurre en un costo de $400.00 ciclo vez que se realiza una corrida de producción, el costo de bodega es de $0.5 unidad por día, y cuando hace falta materia prima existe una perdida de $0.7 unidad por día. a) Cuál seria la cantidad optima a pedir. b) La fondos irrealizables máxima que se presenta .
Solución:
Tamaño económico de distribución, ciclo productivo, faltantes permitidos.
r = 150 sacos/día
k = 250 sacos/día
C3=$400
C1=$0.5 /día
C2=$0.7 /día
a) 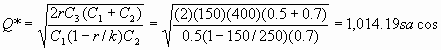
b) 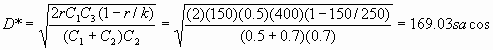
Conclusión: La cantidad optima a producir seria de 1,014 o 1,015 sacos por corrida presentándose una fondos irrealizables máxima de 169 sacos.
PROBLEMA 6. Descuentos por volumen vrs producción
Una empresa de informática se dedica a la venta de computadoras, trata de determinar como minimizar los costos anuales relacionados con la compra de tarjetas de representación para las computadoras, ciclo vez que se hace un pedido se incurre en un costo de $20. El precio por tarjeta de representación depende del número de tarjetas pedidas según la siguiente tabla
| No. de tarjetas pedidas de representación | tasación por tarjetas de representación |
| Q<300 | $10 |
| 300£ q<500 | $9.80 |
| Q³ 500 | $9.70 |
El costo anual de bodega es el 20% del bravura del inventario. Cada mes la empresa de consultaría emplea 80 tarjetas de representación.
POR OTRA PARTE la empresa de informática esta pensando producir las tarjetas de representación como otros componentes que ya fábrica. Ocupa a un empleado que trabaja 4 horas y hambre $3/hora y a una empleada para realizar las llamadas la cual trabaja 1 hora y hambre $3/hora más un tiempo muerto de la máquina que se bravuraa en $20.
El costo por almacenar la tarjetas es de $1.95/año, la empresa puede producir a un ritmo de 100 tarjetas de representación al mes y el precio de ciclo tarjeta producida sale en $9.85.
Se le contrata a usted como Ingeniero para que determine cual es la mejor decisión que minimice los costos para la empresa. ¿Debería la empresa comprar las tarjetas o producirlas?
Solución:
Analizo descuentos por volumen
C3=$20 (costo por ordenar)
C1=0.20*bravura del inventario = 0.20p /año p: precio
r = 80 tarjetas/año = 960 tarjetas / año
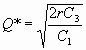
![]()
![]()
![]()
![]()
Miro que Q* si estan en el rango y si son validos o no.
Q*1= 138.56 < 300 SI Q1*=138.56
Q*2= 300 £ 139.97 < 500 NO pero cumplo con los 139.97 no importando que sobre y Q2*=300 (nuevo)
Q*3= 140.69 ³ 500 NO también se cumple lo requerido y el Nuevo Q*3=500
Por lo tanto los tres Q* son validos de las siguiente manera
Q*1=138.56 Q*2=300 Q*3=500
Obtengo costos totales
![]()
![]()
![]()
Por lo tanto para la parte de descuento por volumen conviene pedir 300 tarjetas ciclo vez
Que se le pide al proveedor con un costo anual de $9,766
Análisis para la parte de producir
C1=$1.95 /año (costo de almacenar)
r = 960/año (demanda)
k = 100/ mes =1200 /año (tasa de producción)
C3= costo de ordenar en este caso costo de producir
4 horas 1 empleado y hambre $3/hora = $12
1 hora 1 empleada $3/hora = $3
Tiempo muerto = $20
Total $35
Costo de producir = C3 = $35 por corrida
p= $9.85 (precio de tarjeta)
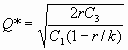
![]()
![]()
![]()
Conclusión:
Al producir el producto la empresa incurrirá en un gasto menor. Lo gastado en descuentos por
volumen seria $9,766/año y al producir seria $9,617.89 y existiría una reducción en
$148.11/año. Por lo tanto esta empresa debería producir las tarjetas de representación.
PROBLEMA 7. Tamaño económico sin faltantes.
Una compañía se abastece actualmente de cierto producto solicitando una cantidad suficiente
para satisfacer la demanda de un mes. La demanda anual del artículo es de 1500 unidades. Se
estima que ciclo vez que hace un pedido se incurre en un costo de $20. el costo de
bodega por inventario unitario por mes es de $2 y no se admite fondos irrealizables.
- Determinar la cantidad de pedido optima y el tiempo entre pedidos
- Determinar la diferencia de costos de inventarios anuales entre la política optima y la política actual, de solicitar un abastecimiento de un mes 12 veces al año.
Solución:
r = 1500 unidades/año
C3 =$20
C1 =$2 unidad/mes = $24 unidad/año
![]()
T=Q*/r = 50/1500 = 1/30 año x 360 jornadas/año = 12 jornadas
Política Actual se le agota ciclo mes o sea 1/12 año
1/12=Q*/1500 Q*=125 (política actual)
![]()
Política Optima
Q*= 50
![]()
Diferencia de $540 por lo tanto se ahora más cuando existe la política optima.
PROBLEMA 8. Tamaño económico de distribución, reabastecimiento instantáneo sin faltantes
Una ferretería tiene que abastecer a sus clientes con 30 sacas de cemento a sus clientes con 30 sacaos de cemento diarios siendo esta una demanda conocida. Si la ferretería falla en la entrega del producto pierde definitivamente el negocio, para que esto no suceda se asume que no existirá fondos irrealizables. El costo de bodega por unidad de tiempo es de Q0.35 unidad al mes y el costo por hacer el pedido es de Q55.00 a) Cuál es la cantidad optima a pedir b)El periodo de agotamiento (asumir 1 mes = 30 jornadas, 1 año = 360 jornadas)
Solución:
r = 30 sacos / día C1= 0.35 unidad / mes
r = 900 sacos / mes C3= Q55
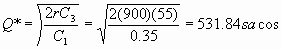
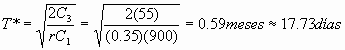 ó T=531.84/30 = 17.73jornadas
ó T=531.84/30 = 17.73jornadas
PROBLEMA 9
Un agente de Mercedes Benz debe pagar $20,000 por ciclo automóvil que compra. El costo anual de bodega se calcula en 25% del bravura del inventario. El agente vende un promedio de 500 automóviles al año. Cree que la demanda se acumula, pero calcula que si carece de un automóvil durante un año, perderá hambrencias futuras por $20,000. Cada vez que coloca un pedido de automóviles, sus costos suman $10,000. a) Determine la política óptima de pedidos del agente b) ¿Cuál es la fondos irrealizables máxima que se presentará?
p = $20,000 p: precio
C1=0.25xbravura del inventario = 0.25p C1=0.25(20,000)=$5,000
C2=$20,000 / año
C3=$10,000
r = 500 / año
![]()
![]() carencia máxima
carencia máxima
![]() (nivel máximo de inventario)
(nivel máximo de inventario)
# pedidos = 500/50 = 10 pedidos al año.
CT= Costo de almacenar + Costo de ordenar + Costo de fondos irrealizables
![]()
![]()
PROBLEMA 10. Descuentos por volumen vrs producción
Un distribuidor de artículos marinos compra tanques de gas a un fabricante, el fabricante ofrece 5% de descuento en ordenes de 15 o más y un 10% de descuento en ordenes de 100 o más. El distribuidor estima sus costos de ordenar en $5 por orden y los de conservación en un 10% del precio del producto, el distribuidor compra 300 tanques por año, determine cual es el volumen de compra que minimiza el costo total, el precio unitario de ciclo tanque es de $12.
Solución:
| tasación Unitario | Cantidad |
| 12 | 0<q<15 |
| 11.40 | 15£ q<100 |
| 10.80 | q³ 100 |
C3= $5
C1=0.10p unidades/año
C2= no existe
![]() X no valido
X no valido
![]() / aceptable
/ aceptable
![]() / aceptable pero con nuevo Q*3=100
/ aceptable pero con nuevo Q*3=100
3CT1= X no admisible
![]()
![]()
el mejor es el 3 porque tiene menor costo Q* = 100 artículos marinos CT=3,309 /año.
Si se realizara una comparación entre 2 modelos el anterior y uno que produce 450 al año a un costo de $6 por ciclo corrida y el costo de almacenar fuera $1.15/año, el precio de $11.70 por ciclo unidad y la misma demanda que el anterior. ¿Qué opción seria mejor producir o comprar?
Solución:
C3=$6 precio = $11.70 K = 450/año
C1=$1.15 /año r = 300/año
![]()
![]()
Conclusión:
Por lo tanto sería mejor comprar ya que al producir gasto más.
Elías Felipe Nij Patzán
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA
FACULTAD DE INGENIERIA
ESCUELA DE MECANICA INDUSTRIAL
ÁREA DE METODOS CUANTITATIVOS Y ECONOMIA
INVESTIGACIÓN DE OPERACIONES 2

Euroinnova

Euroinnova
