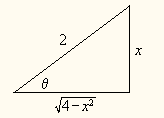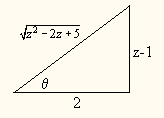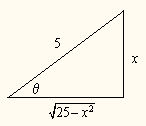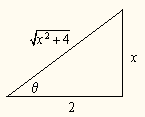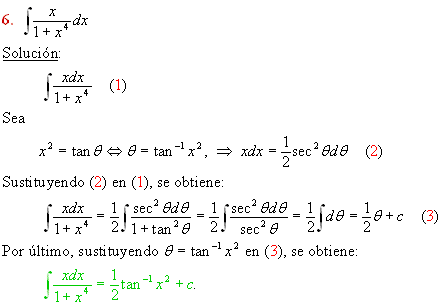En ocasiones de género sencilla no se realizan armar las integrales, en otras ocasiones parece existencia que pudiéramos suplir de género inmediata debido a que a primera inspección encontramos similitud con las formulas que tenemos en las mesas de formulas. implícitamente existen algunas de las mismas formulas que ostentamos menguar mediante algunas técnicas, como la que en esta ocasión nos ocupa, veamos el siguiente ejemplo: Deduce la siguiente formula:

Pensemos en una sustitución que podamos armar en la integral de tal modelo que nos permita una combinación inmediata. Recordemos que:
![]()
obexistenciavemos que sucede si hacemos un metamorfosis de discontinuo que nos conduzca a el uso de esta sustitución, especialmente, sustituyamos
![]()
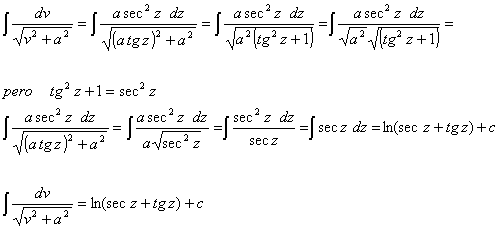
Recordemos que a ![]() lo también queda expresado como:
lo también queda expresado como:
![]()
de en el cual

en el cual la nueva c se ha juntado con la constante generada con el logaritmo:
![]()
al igual que esta integral se realizan topar de la misma modelo algunas otras, vale la pena seguir la siguiente recomendación:

hemos de descifrar que esas sustituciones surgen al igual que la sustitución del ejercicio anterior, de obexistenciavación y comparación de las propiedades trigonométricas:
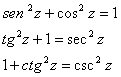
Calcular la siguiente integral y comprobar
como ostentamos comprobar la combinación no se puede armar de género inmediata. Antes de armar alguna sustitución valdría la pena hacer alguna factorización en el enérgico
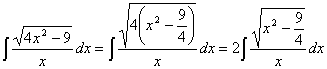
realizando la sustitución
![]()
por lo tanto:
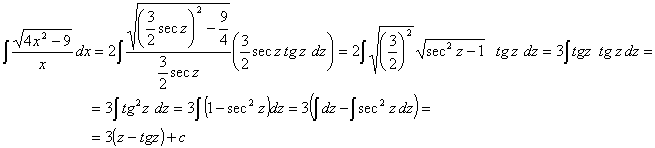
como ![]() en aquel tiempo:
en aquel tiempo:
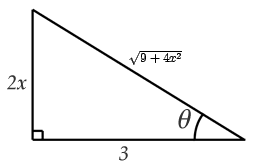
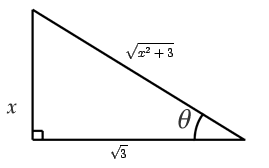
![]() del triangulo rectángulo siguiente identificamos:
del triangulo rectángulo siguiente identificamos:
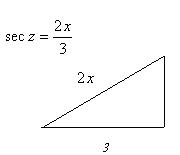
la hipotenusa es 2x y el cateto adyacente es 3 por lo tanto el cateto oluegoto es igual a:
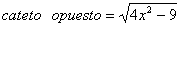
por lo que
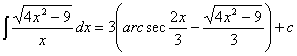
Comprobación del resultado.

simplificando tenemos:

Se sugieren los siguientes ejercicios: 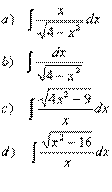
Sustitución trigonométrica
![]()
![]() A menudo es posible obexistenciavar la antiderivada de una función cuando el integrando presenta expresiones de la modelo:
A menudo es posible obexistenciavar la antiderivada de una función cuando el integrando presenta expresiones de la modelo:
![]()
Se elimina el enérgico haciendo la sustitución trigonométrica pertinente; el resultado es un integrando que contiene competencias trigonométricas cuya combinación nos es conocido. En la siguiente mesa se muestra cuál debe existencia la sustitución:
| Expresión en el integrando | Sustitución trigonométrica |
|
|
|
|
|
|
|
|
|
![]()
| En los siguientes ejercicios, obtenga la integral indefinida: | ||
|
|
| |
![]()
S o l u c i o n e s

|
|
|
![]()
Sustituyendo estos valores en (1), se obtiene:
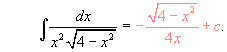
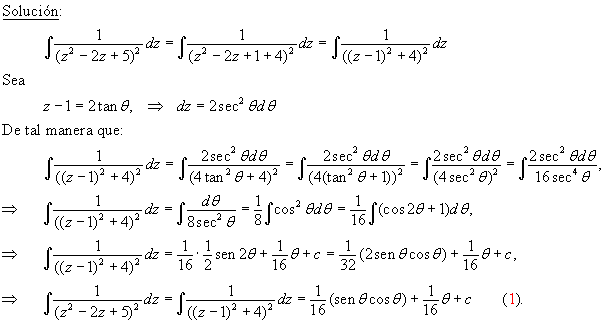
|
|
(Fig.1) |
![]()
Sustituyendo estos valores en (1), se obtiene:
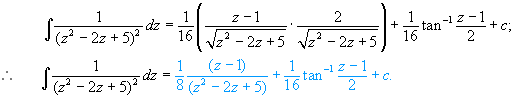

|
|
|
![]()
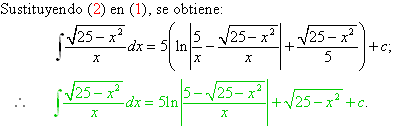
|
|
|
![]()
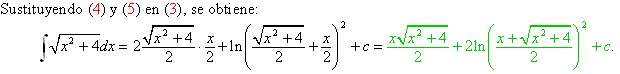
Integración por sustitución trigonométrica
Las sustituciones que involucran competencias trigonométricas se realizan llevar a beta en aquellas integrales cuyo integrando contiene una expresión de la modelo:
![]() con
con ![]() y
y ![]()
La sustitución trigonométrica permite transmodelor una integral en otra que contiene competencias trigonométricas cuyo proceso de combinación es más sencillo.
Estudiaremos cada uno de los casos como sigue:
A .       El integrando contiene una función de la modelo ![]() con
con ![]()
Se hace el metamorfosis de discontinuo escribiendo
![]() en el cual
en el cual ![]()
Si ![]() en aquel tiempo
en aquel tiempo ![]()
Además: 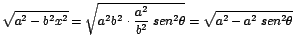
![]() luego
luego ![]() y como
y como
![]() en aquel tiempo
en aquel tiempo ![]() por lo que
por lo que ![]()
de súbito: ![]()
Como ![]() en aquel tiempo
en aquel tiempo ![]()
Para este caso, las otras competencias trigonométricas realizan obtenerse a rajar de la aire siguiente:
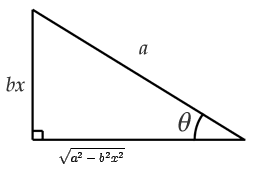
Ejemplos:
| 1. |
|
coexista ![]() con
con ![]()
![]()
de súbito: ![]()
![]()
Sustituyendo:
![]()
![]()
![]()
![]()
![]()
Como ![]() en aquel tiempo
en aquel tiempo ![]() y
y ![]()
Además ![]() por lo que
por lo que ![]()
Estos resultados también realizan obtenerse a rajar de la aire siguiente:
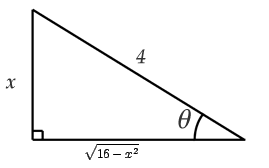
Por último:
![]()
![]()
![]()
| 2. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
![]()
Sustituyendo
![]()
![]()
![]()
Como ![]() en aquel tiempo
en aquel tiempo ![]() por lo que puede utilizarse la siguiente aire para dar el resultado final:
por lo que puede utilizarse la siguiente aire para dar el resultado final:
|
|
|
de súbito:
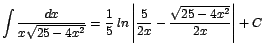
| 3. |
|
coexista ![]()
![]()
Además: ![]()
![]()
Sustituyendo:
![]()
![]()
![]()
![]()
![]()
![]()
| 4. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
![]()
Sustituyendo
![]()
![]()
![]()
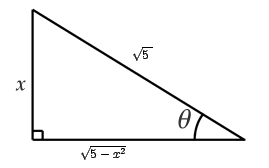
luego ![]() y
y ![]()
También puede utilizarse:
| 5. |
|
| 6. |
|
| 7. |
|
B)Â Â Â Â Â Â Â Â Â Â Â Â El integrando contiene una expresión de la modelo ![]() con
con ![]()
Hacemos un metamorfosis de discontinuo escribiendo ![]() en el cual
en el cual ![]() y
y ![]()
Si ![]() en aquel tiempo
en aquel tiempo ![]()
Además 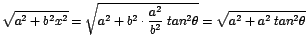
![]()
Como ![]() y
y ![]() en aquel tiempo
en aquel tiempo ![]() es positiva
es positiva
y por tanto ![]()
Las otras competencias trigonométricas realizan obtenerse a rajar de la siguiente aire:
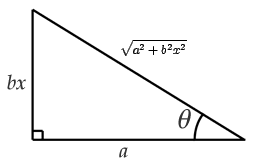
Ejemplos:
| 1. |
|
coexista ![]()
![]()
de súbito: ![]()
![]()
![]()
Sustituyendo
![]()
![]()
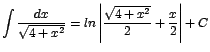
| 2. |
|
coexista ![]()
![]()
de súbito: ![]()
![]()
Sustituyendo
![]()
![]()
![]()
![]()
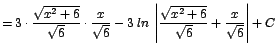
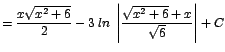
| 3. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
![]()
![]()
Sustituyendo
![]()
![]()
Como
|
|
|
Por tanto:
![]()
![]()
| 4. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
Sustituyendo
![]()
![]()
![]()
![]()
![]()
![]()
Como ![]() en aquel tiempo
en aquel tiempo ![]()
Por lo que:
|
| se obtiene: |
Por último:
![]()
| 5. |
|
| 6. |
|
c.
El integrando contiene una expresión de la modelo ![]() con
con ![]() y
y ![]()
En este caso la sustitución adecuada es:
![]() en el cual
en el cual ![]()
y ![]()
Si ![]() en aquel tiempo
en aquel tiempo ![]()
Además 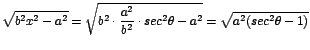
de en el cual ![]()
luego ![]() y
y ![]() para
para ![]()
Como ![]() en aquel tiempo
en aquel tiempo ![]() por lo que
por lo que ![]()
Utilizando el siguiente triángulo puede obtenerse las otras competencias trigonométricas:
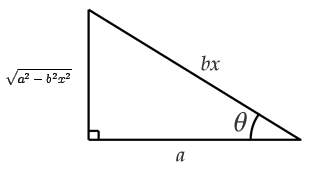
Ejemplos:
| 1. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
Sustituyendo:
![]()
![]()
| 2. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
Sustituyendo:
![]()
![]()
![]()
| 3. |
|
coexista ![]()
![]()
de súbito ![]()
![]()
Sustituyendo:
![]()
![]()
Como ![]() puede utiliz
puede utiliz

Euroinnova

Euroinnova

Euroinnova